 Elliptic Curve Cryptography
Elliptic Curve Cryptography
template 0.2 | 240728
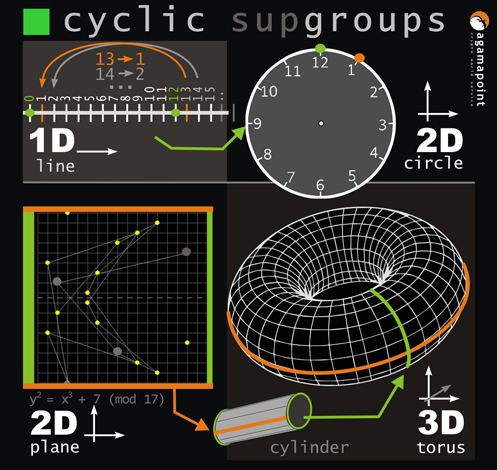
In group theory, a cyclic group is defined as a group generated by a single element called a generator.
By repeatedly applying special operations to this element, all elements of the group, including the identity element,
are obtained. This concept resembles modular arithmetic, where elements return to the initial state after
a specific number of operations, demonstrating the cyclical nature of both structures.
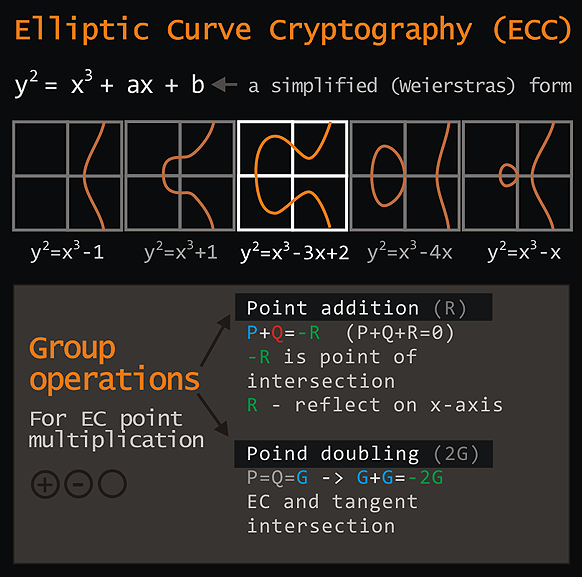
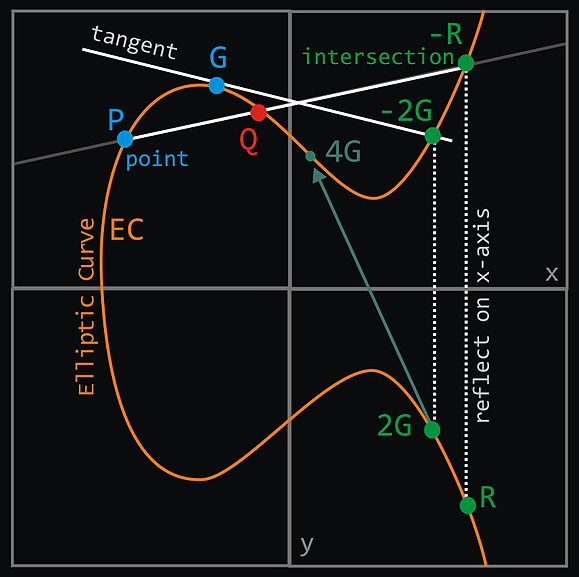
The image depicts adding elements by connecting points with a line, graphically interpreting inversion across the x-axis,
and doubling an element using a tangent line to an elliptic curve. These geometric methods illustrate operations in elliptic curve cryptography, where point addition and doubling are fundamental to the curve's algebraic structure.
+ --- DH --- + --- EC ---+ | 2380 bit | 228 bit | ----------------+--------------- | G represent secret | | as a number | as a point | ----------------+---------------Diffie-Hellman (2380-bit) uses large numbers for secure key exchange, whereas Elliptic Curve Diffie-Hellman (ECDH, 228-bit) uses elliptic curve points, offering similar security with smaller keys, faster computations, and greater efficiency.
BTC
Bitcoin: secp256k1 (specification for an elliptic curve used in cryptography) ================== G: G[0]=0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798 G[1]=0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8 (Bit size: 256) p = (2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 -1) = (2**256 - 2**32 - 977) = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f = 115792089237316195423570985008687907853269984665640564039457584007908834671663 ... len(int(p)) = 78 | 17 x 17 cm versus "the universe is too small" ~ Proxima centauri 3,99×10**13km = *10**9m -> 10**22 ~ pulsar ULAS J1342+0928 1.239×10**14km -> 10**23 mm! a: 0 | b: 7 =========== and where the field (p) is the prime number used with: y² = x³ +7 (mod p) Q = (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424) x, y = Q[0], Q[1] xx = (x ** 3 + 7 - y**2) % p # substitute the values into the curve equation print(xx) -> 0 Proof that a point (public key Q) lies on the curve is first basic validation.