Kryptografie

Kryptografie neboli šifrování je nauka o metodách utajování smyslu zpráv převodem do podoby, která je čitelná jen se speciální znalostí. Slovo kryptografie pochází z řečtiny – kryptós je skrytý a gráphein znamená psát.
Tolik Wikipedie – ve zkratce.

Šifry, rébusy a matematika

.:.

Na obrázku vpravo vidíte v kruhu trojici trojúhelníků, kterými byl fascinovaný Tesla. Mimochodem časový průběh trojfázového proudu má analogické zobrazení. On byl ale symbolikou čísel (speciálně trojkou) úplně uhranutý:

If you only knew the magnificence of the 3, 6 and 9, then you would have the key to the universe. (Nikola Tesla)

1 + 4 + 7 = 12   | 1 + 2 = 3
2 + 5 + 8 = 15   | 1 + 5 = 6
3 + 6 + 9 = 18   | 1 + 8 = 9
posloupnost 3 6 9 ...ciferné součty, které nemohou být "náhoda"?

…a navíc, číslo je dělitelné třemi, pokud jeho ciferný součet je také dělitelný třemi.

Prvočísla, magické čtverce a teorie všeho

Prvočíslo je beze zbytku dělitelné jen číslem jedna a sebou samým.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101 …
Jediné sudé prvočíslo je 2.
https://maths.cz/clanky/138-prvocislo – jeden z mnoha článků…
Zajímavé je rozložení (hustota) prvočísel: http://hradec.org/idnes/primes.html

Mersennova prvočísla Mn jsou vzácná prvočísla, která lze zapsat ve tvaru 2 na n-tou minus 1. Rekordní prvočíslo (2016) má zhruba o pět miliónů víc číslic než dosavadní držitel rekordu. Číslo s označením M74207281 vygeneroval (ověřil) superpočítač za několik dní. Má přesně 22 338 618 číslic a vzniklo vzájemným znásobením 74 207 281 dvojek a následným odečtením jedničky (dle definice).

.:.

Matematické (i fyzikální) konstanty – Ludolfovo číslo (π [pí]) nebo Eulerovo číslo (e) – se stejně jako specifické matematické řady (prvočísla, fibonaciho posloupnost…) v šifrování využívají. Jsou to „tabulky“ které mají k dispozici odesílatel i příjemce zprávy. Při prolomení šifry jsou ale „zdiskreditované“. Proto se užívají specifické dlouhé klíče (třeba pokud má poslední prvočíslo k dispozici pouze vláda a její tajná služba, jeho nalezení nebo ověření zabere nejvýkonnějším počítačům spoustu času (i roky) a je proto i při vyzrazení stále dobrým klíčem).

Některá „kouzelná“ čísla a rovnice:
Prvočíslo (Prime number) označíme v poznámece [P].

circular prime – samostané dílčí trojice jsou také [P]
193 939 | 939 391 | 393 919 | 939 193 | 391 939 | 919 393

emirp – jak z názvu napovídá je prime čteno pozpátku:
13 – 31 | 17 – 71 | 37 – 73 | 79 – 97 | 107 – 701 | …

čtyři po sobě jsoucí číslovky?
4567 [P]

prvních n číslovek je dělitelno n-tým prvočíslem? toto je největší prvočíslo:
8 757 193 191 [P]
8:2, 87:3, 875:5, 8757:7, … :11, …

největší Fibonachiho číslo, které je také prvočíslem?
F104911

další hezká prvočísla
799999999 [P]
4332221111 [P] 1×4,2×3, 3×2, 4×1
51413 [P] reverse prvních 5 číslovek pí

narcistická čísla? součtem třetích mocnin svých tří cifer
153 = 1³ + 5³ + 3³
370 | 371 | 407

π .10⁷ tolik má rok zhruba vteřin (31415926)

Magický čtverec zpravidla obsahuje posloupnost (neopakujících se) čísel a má nějaké zajímavé vlastnosti – nejčastěji: součet sloupců, řádek i uhlopříčky je vždy stejné číslo.

2 7 6     |    4 9 2
9 5 1     |    3 5 7      (pootočená varianta) 
4 3 8     |    8 1 6
...řádky, sloupce i uhlopříčky mají součet 15. Také hezké fragmenty pro PINy.

https://cs.wikipedia.org/wiki/Magick%C3%BD_%C4%8Dtverec

.:.

Jednoduché záměny – substituce a transpozice

Caesarova šifra

Tuto šifru používal pro vojenskou komunikaci Julius Caesar a popsal ji v Zápiscích o válce galské. Používal posun o tři místa, obecně je ale za Caesarovu šifru označováno jakékoli šifrování na principu prostého posunu písmen (znaků) o konstantní hodnotu.

Jednoduchým způsobem zaměníme znaky za posunuté. Například Posun 1 by znamenal, že místo A píšeme B, namísto B pak C, a tak dále. A >B, B->C, D->E.
AGAMA (1) = BHBNB.
Známou abecedu máme jednoznačně seřazenou (ABCDEFGHILKL…) a tak můžeme snadno kódovat i dekódovat. Posun 2 je pak obdobně A->C, B->D, …
AGAMA (2) = CICOC.

Oblíbená „prohazovačka“ (záměna jednoho znaku za jiný) používaná na geocaching je vlastně Ceasarova šifra s posunem 13.
Zde máte funkční skript, pro všechny možné posuny (přednastaveno na zmíněnou „polovinu“: 13). Historicky používáme jen velká písmena (podle řeckých) – takže pozor na „case sensitive“ u hesel, kde zase defaultně dominují písmena malá.

Decryption Key 
A|B|C|D|E|F|G|H|I|J|K|L|M
-------------------------
N|O|P|Q|R|S|T|U|V|W|X|Y|Z 
(letter above equals below, and vice versa)

.:.

Šifra je to velmi slabá, v tomto skriptu nám ani nefunguje na čísla, ale v případě unikátního přenosu jednoho hesla se v kombinaci s dalším „zamícháním“ dá v pohodě použít (vždy je to lepší než nic). A také „zamotá hlavu webovým robotům“, co odchytnou jen zašifrovanou zprávu a v základu pak není na první pohled poznat ani o co jde.

Involuce

Involutivní operace (nebo involuce) je funkce fff, která splňuje f(f(a)) = a pro všechny hodnoty a v její „doméně“.
To znamená, že aplikace operace fff dvakrát za sebou vrátí původní hodnotu a.

Negace
Reverse (otočení řetězce)
Bitová operace XOR s konstantou
Permutace s vlastností involuce
ROT-13 (Caesar)
github.com/octopusengine/linux/…/code_cypher.md

U jednoduchých tabulek záměn je trochu problém, že musí být jednoznačně dáno, která tabulka se použila. Mohou se lišit značením, prohozením sloupců a řádek nebo vypuštěním méně frekventovaných písmen (pro matici 5×5 při 26 znacích vypouštíme CH / Q / W=V / J=I / …
ABCDE/12345 může být AXYZF/01238 … a také víceznakové, kde se vybírá jedna z možností.
Některým variantám se říká „šachová šifra“ a používá se opakující se patern v matici 8×8, protože připomíná zápis šachové partie (což ale šachista okamžitě prokoukne, že to tak není).

polybios code:

- 1 2 3 4 5
1 A B C D E
2 F G H I K
3 L M N O P
4 Q R S T U
5 V W X Y Z
J=I

- 1 2 3 4 5
1 A F K P V
2 B G L R W
3 C H M S X
4 D I N T Y
5 E J O U Z
Q .. x

- 1 2 3 4 5
A A B C D E
B F G H I J
C K L M N O
D P R S T U
E V W X Y Z
(A1)

. . .

:::

http://www-math.ucdenver.edu/~wcherowi/courses/m5410/m5410cc.html
částečná záměna http://sifry.sourceforge.net/abc_subs_password.html

abc

Předchozí část by také mohla sloužit ke generování hesel.

Kdysi doporučované:
Str0nG P45w0rD (leetspeak)
už spadá do Security through obscurity.

Vaše přístupová hesla na nějaký server musí být uložena i na tom serveru. Ale to se ukázalo jako velká zranitelnost, proto jsou hesla na serveru ukládána „zahašovaná“ (hash). Například MD5 ale už velký počet hesel má „prolomen“, stačí ukrást databázi „hašů“ a hledat heslo, které k tomu padne.
Například „abc“ má MD5_hash: 900150983cd24fb0d6963f7d28e17f72
A stačí se zeptat googla:
https://md5.gromweb.com/?md5=900150983cd24fb0d6963f7d28e17f72 a od nám odpoví, že heslo je „abc“.

Všechna tří a čtyřznaková byla zdokumentována už před několika lety a pak jsou nějaká častá (a proto slabá) hesla – například pár stovek prolomených ukázek: https://cavac.at/guest/security/bad_passwords.txt.

Symetrická a asymetrická

…
Cézarova šifra – jednoduché posunutí o několik znaků
(symetrická – klíč je shodný pro odesílatele i příjemce)
Vernam – dynamické posunutí (pro každý znak jinak)
Otočná mřížka…

asymetrická – pár klíčů: soukromý a veřejný
…

využití je více trochu rozebráno: agamapoint.com/vybrane-terminy/

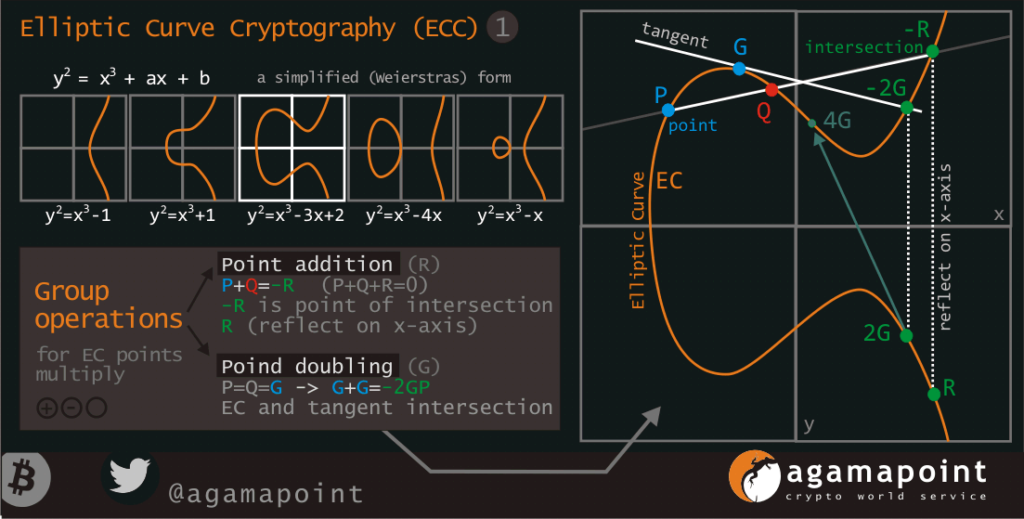
Eliptické křivky

V bodech a odkazech

> agamapoint.com/cypherpunk/
Phil Zimmermann (krypto guru)
philzimmermann.com – jeden z úvodů do kryptografie

kryptomeny-bitcoin-litecoin – obsáhlý článek (na volné noze)
visual-secure – grafické skládání klíčů
crypt-file: Hans – jeden za našich programů, na kryptování

Enigma – šifrovací stroj – hodně ovlivnil průběh světové války
Viribusunitis – stránky kamaráda, co staví šifrovací stroj
Otočná mřížka – používáme také

Bitcoin je nesmrtelný – vy ne – jak zajistit správné předání
Secret messages – python – jednoduché kryptování zpráv

metal-bitcoin-seed-storage-stress-test test kovových „master seedů“
bunkeroid.com | cryptosteel | cryptokeystack | coldti
octopusengine.org | trezor.io | blockchainlegal.cz
…

síla hesla: https://cs.wikipedia.org/wiki/S%C3%ADla_hesla

Vybrané kódování, šifry a pomůcky

Morse – iN FOr mA CE vN osné
Polský kříž
http://www.shaman.cz/sifrovani/velky-polsky-kriz.htm
Cézarova šifra – jednoduchá záměna (posun / prohození)
https://github.com/octopusengine/agama_point_crypto/blob/main/test_cipher_caesar.py
Vigenèrova šifra (Le chiffre indéchiffrable)
text se šifruje pomocí série různých Caesarových šifer v závislosti na písmenech klíče
https://cs.wikipedia.org/wiki/Vigen%C3%A8rova_%C5%A1ifra
Polybiův čtverec – matice 5×5, znaky na čísla – 11=A…
https://www.dcode.fr/polybius-cipher
https://github.com/octopusengine/agama_point_crypto/blob/main/test_cipher_polybius.py
Fleissnerova mřížka (otáčecí mřížka)
http://www.musilek.eu/michal/sifry-fleissner.html?menu=cc&item=s&lang=cz
https://github.com/octopusengine/agama_point_crypto/blob/main/test_cipher_fleissner.py
https://www.thingiverse.com/thing:4747160
MD5, AD..
PGP (Pretty Good Privacy), AES, …
SSSS

V prvních fázích hry používáme pouze 1-6 a snaha bude moc to nekomplikovat. Pár návodů mezi klasickými „dětskými“ rébusy: pruzkumnik.cz/praxe/sifry

Pár dalších odkazů:
https://www.agamapoint.com/aes/
http://crypto-world.info/
http://www.musilek.eu/michal/sifry.html?menu=cc&lang=cz
(Fleissnerova mřížka z čísla: 214321134421)

Python:
https://rpubs.com/mstefan-rpubs/ciphers
https://github.com/octopusengine/crypto_agama/blob/main/crypto_agama/cipher.py

Menu