big-numbers

Velká čísla jsou pro lidskou mysl často těžko uchopitelná, protože naše každodenní zkušenosti zahrnují spíše menší, konkrétní hodnoty. Jakmile začneme mluvit o miliardách, bilionech nebo ještě větších číslech, ztrácíme intuitivní představu o jejich velikosti. Proto se často uchylujeme k analogiím, které nám pomáhají lépe porozumět těmto rozměrům.
Například když porovnáváme velikost Slunce s pomerančem nebo vzdálenost mezi hvězdami s obrovskými vzdálenostmi na Zemi, usnadňujeme si pochopení vesmírných a matematických konceptů. Analogiemi převádíme abstraktní čísla do něčeho, co můžeme lépe vnímat.
…
| Exponent (10n) | Předpona | Značka | Název | Původ | |
| 103 | kilo | k | tisíc | řec. χίλιοι – „tisíc“ | |
| 106 | mega | M | milion | řec. μέγας – megas „velký“ | |
| 109 | giga | G | miliarda | řec. γίγας – gígas „obrovský“ | |
| 1012 | tera | T | bilion | řec. τέρας – teras „netvor“ | |
| 1015 | peta | P | biliarda | řec. πέντε – pente „pět“ | 5 * 3 = 15 |
| 1018 | exa | E | trilion | řec. ἕξ – hexa „šest“ | 6 * 3 = 18 |
| 1021 | zetta | Z | triliarda | fr. sept – „sedm“ | 7 * 3 = 21 |
| 1024 | yotta | Y | kvadrilion | řec. ὀκτώ – okto „osm“ | … |
| 1027 | ronna | R | kvadriliarda | řec. a lat. – ‚ennea‘ a ‚novem‘ – „devět“ | |
| 1030 | quetta | Q | kvintilion | lat. decem – „deset“ | |
| … |
Pár jednoduchých úvah pro základní představu
Kolik je milión vteřin?
Milión sekund se rovná přibližně 11,57 dní. (Necelých 12 dní). To zjistíme jednoduchým výpočtem: 1 den má 24 hodin, každá hodina 60 minut, a každá minuta 60 sekund.
Takže:
1 den = 24 × 60 × 60 = 86 400 sekund.
Milión vteřin je tedy 1 000 000 ÷ 86 400 ≈ 11,57 dní.
Kolik je jedna miliarda vteřin?
Jedna miliarda vteřin odpovídá přibližně 31,7 rokům. Postupujeme obdobně jako u miliónu:
1 rok ≈ 365,25 dnů × 24 × 60 × 60 = 31 557 600 sekund.
Miliarda vteřin tedy je:
1 000 000 000 ÷ 31 557 600 ≈ 31,7 let. Dalo by se říci skoro 32 let.
Jaký objem má Země?
Objem Země lze spočítat podle vzorce pro objem koule:
V = 4/3 π r3, kde r je poloměr Země (přibližně 6 371 km).
Objem Země tedy je:
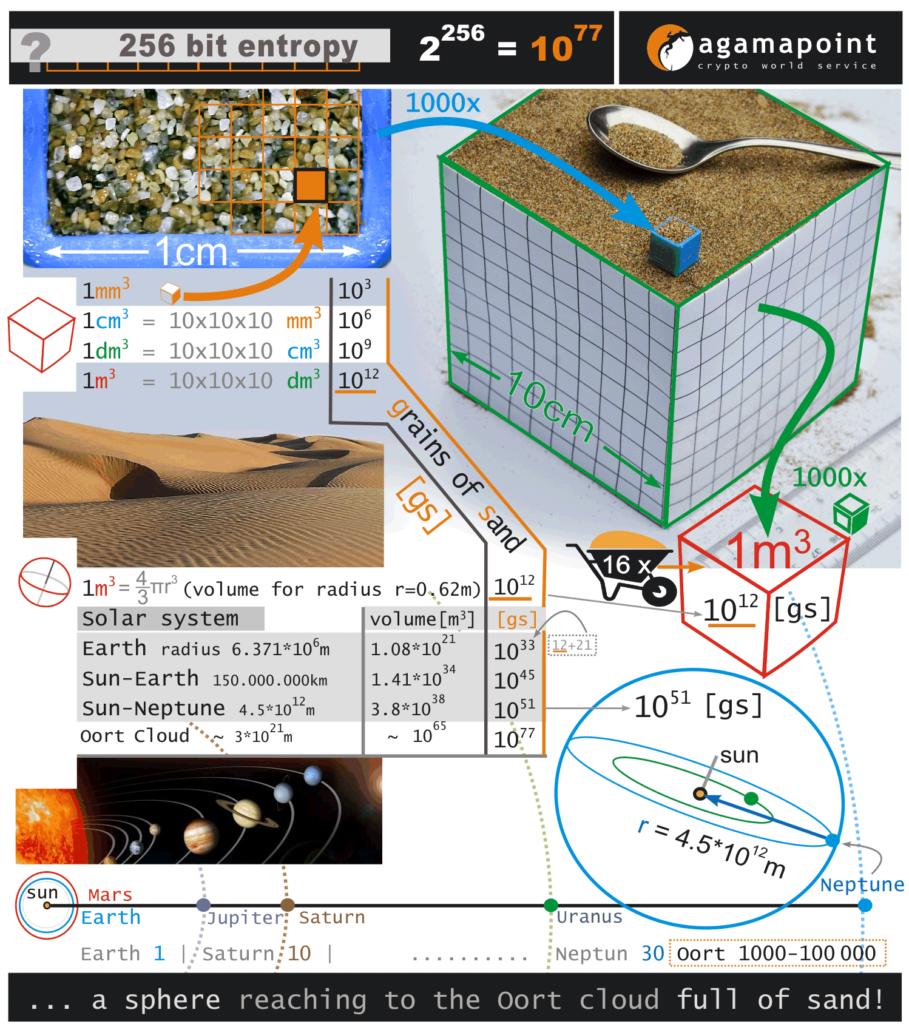
V ≈ 4/3 π (6 371 × 103)3 ≈ 1,08 × 1021 m3.
To znamená, že Země má objem přibližně 1,08 kvintilionu kubických metrů.
Jaký objem má Slunce?
Objem Slunce, stejně jako u Země, vypočítáme pomocí vzorce pro kouli. Poloměr Slunce je přibližně 696 340 km:
V ≈ 4/3 π (696 340 × 103)3 ≈ 1,41 × 1027 m3.
Slunce má tedy objem přibližně 1,41 sextilionu kubických metrů, což je přibližně 1,3 milionkrát více než Země.
Jak dlouhý je světelný rok a kolik m3 zabere koule s tímto poloměrem?
Světelný rok je vzdálenost, kterou světlo urazí za jeden rok, což je přibližně 9,46 bilionů kilometrů (9,46 × 1012 km). Objem koule o poloměru světelného roku můžeme opět spočítat jako:
V = 4/3 π r3, kde r = 9,46 × 1012 km = 9,46 × 1015 m.
Objem takové koule je:
V ≈ 4/3 π (9,46 × 1015)3 ≈ 3,55 × 1048 m3.
Tato koule by měla objem asi 3,55 kvadrilionu kvadrilionů kubických metrů.
Exponenty se používají k vyjádření velkých čísel pomocí mocnin.
Při násobení čísel se stejným základem se exponenty sčítají.
Jinými slovy, pokud máme dvě čísla ve tvaru am a an, kde a je základ a m a n jsou exponenty, jejich násobení vypadá takto:
am × an = am+n
Například: 103 × 106 = 103+6 = 109, což vyplývá i z tabulky pro „předpony“: miliarda je tisíc miliónů.

Poloměr námi pozorovatelného vesmíru je odhadován na přibližně 46,5 miliard světelných let (ly). To zahrnuje vzdálenosti objektů, které můžeme v současnosti pozorovat, i když světlo, které k nám přichází, pochází z doby krátce po Velkém třesku.
V kilometrech je poloměr vesmíru výrazně větší. Jeden světelný rok je přibližně 9,46 bilionů kilometrů, takže poloměr vesmíru v kilometrech můžeme vypočítat:46,5 miliard sveˇtelnyˊch let×9,46×1012 km/sveˇtelnyˊ rok=4,4×1023 km46,5 \, \text{miliard světelných let} \times 9,46 \times 10^{12} \, \text{km/světelný rok} = 4,4 \times 10^{23} \, \text{km}46,5miliard sveˇtelnyˊch let×9,46×1012km/sveˇtelnyˊ rok=4,4×1023km
Takže poloměr pozorovatelného vesmíru je asi 4,4 × 10²³ kilometrů.
což je přibližně 4,4 × 10²⁹ milimetrů.

2**128
>>>340282366920938463463374607431768211456
=3.4 * 10 ** 38
2**256
>>>115792089237316195423570985008687907853269984665640564039457584007913129639936
=1.1 * 10** 77