Ukázky kódu
Vybrané části jednoduchých skriptů -někdy i lehce detailněji
Začínáme čistě Linuxovým shellem, postupně je něco i v Pythonu nebo Go.
Entropie | Chaos | WIF | BIPs |
SHA | ECC | D-H | AES | …
HASH – SHA-2 | SHA256 (Secure Hash Algorithm)
http://www.abclinuxu.cz/clanky/decentralizovana-kryptomena-bitcoin
2011 – psáno pro Linuxáky a trochu programátory
~$ echo -n „AgamaPoint“ | sha256sum 29b5a9c21f25fcc7c015fee558aa15dd28341487e76ac744583adb37eda1e2f7
Hledání „nonce“ jako základ miningu (proof of work), jako hledání „malého čísla“ HASHe (začíná několika nulami, podle obtížnosti):
~$ i=0; while ! (echo -n "Agama Point $i" | sha256sum | tr -d "\n"; echo " (nonce=$i)")|grep -E "^00"; do let i++; done (chvíle počítání) 00999ac48b71fc267a67f78bb379d554020d062343d344269d62d4b9f55b90b1 - (nonce=263)
Python implementace SHA256, pro „porozumění“, jak to funguje
https://github.com/agama-point/agama_point_crypto/blob/main/crypto_agama/sha256py.py
.:.
Hash hraje důležitou roli i v komunikačním protokolu SSL/TLS (Secure Sockets Layer/Transport Layer Security)
Tabulka bezpečnosti a odhalených „kolizí“: https://valerieaurora.org/hash.html
https://developer.bitcoin.org/devguide/mining.html
ssss – Shamir’s Secret Sharing Scheme
K dešifrování zprávy, potřebujeme alespoň t klíčů z n vygenerovaných.
~$ sudo apt install ssss ... ~$ ssss-split -t 3 -n 5 Generating shares using a (3,5) scheme with dynamic security level. Enter the secret, at most 128 ASCII characters: Using a 144 bit security level. 1-ba1e20615599c30c26b6827e8646a9197d48 2-136052b42a8d1dfc73706718be73da51181e 3-c51f643028f8ed820561cc1ae7211245b714 4-dd9f3b224b0557a528d9d43752d3ba62146b 5-0be00da64970a7db5ec87f350b817276bb73 ... ~$ ssss-combine -t 3 Enter 3 shares separated by newlines: Share [1/3]: 1-ba1e20615599c30c26b6827e8646a9197d48 Share [2/3]: 3-c51f643028f8ed820561cc1ae7211245b714 Share [3/3]: 5-0be00da64970a7db5ec87f350b817276bb73 Resulting secret: kobyla ma maly bok
Transaction
vzhledem k rozsahu – máme samostatnou stránku: https://www.agamapoint.com/transakce/
BIP / Python
https://github.com/blockstack/pybitcoin
https://pypi.org/project/python-bitcoin-tools/
https://github.com/petertodd/python-bitcoinlib
>>>
sr-gi/bitcoin_tools – https://github.com/sr-gi/bitcoin_tools (má i testnet)
>>>
zdroj BTC „core“ na githubu: https://github.com/bitcoin/bitcoin
ECC & bitcoin

Asymetrická kryptografie (kryptografie s veřejným klíčem) je v informatice typ kryptografických algoritmů, ve kterých se používá dvojice kryptografických klíčů. Algoritmus využívá jednosměrnou funkci, která znemožňuje použití stejného klíče pro šifrování i dešifrování. Tím se odlišuje od symetrické kryptografie, která používá jediný klíč. V asymetrické kryptografii je jeden klíč soukromý (privátní, „tajný“) a druhý veřejný, jehož pravost může být ověřitelná. (Wiki)
Jak z privátního klíče (generovaného „z velké entropie“) získat klíč veřejný?
Mělo by to být snadno matematicky a jednoznačně (pro dané parametry pokaždé stejně) „vypočítatelné“.
2n = 1024 | 2 * 2 * 2 * …. kolikrát * 2 = 1024
n = 10, protože 1024 = dvě na desátou a je snadné získání „tajného čísla“ n pomocí logaritmu.
log2(1024) = n
Dískrétní logaritmus? | pomocí modulo / mod / %
2n mod 17 = 4
? to už tak jednoznačné není, kdy navíc v tomto jednoduchém případě to platí pro nekonečně velkou množinu řešení n:
(2, 10, 18, … „až do nekonečna“)
for i in range(1, 21):
print(f'{str(i).rjust(3)}{str(2**i).rjust(7)}{str((2**i)% 17).rjust(5)}')
"""
1 2 2
2 4 4
3 8 8
4 16 16
5 32 15
6 64 13
7 128 9
8 256 1
9 512 2
10 1024 4
11 2048 8
12 4096 16
13 8192 15
14 16384 13
15 32768 9
16 65536 1
17 131072 2
18 262144 4
19 524288 8
20 1048576 16
""" Diffie-Hellman
Jak se ověří, že někdo zná klíč, aniž by ho prozradil?
Výměna klíče k dešifrování je nejslabším místem kryptografie. Proto se zavádí možnost výměny veřejných klíčů (které si každý z účastníků sám ověří nebo přímo vytvoří).
n = 17 # p
G = 71 # G
def dh(sk, g=G):
pk = g ** sk % n
# print(n, g, g ** x, pk)
print(g, f'({str(sk).rjust(3)}) -> {str(pk).rjust(5) }')
return pk
print("="*30)
print("Alice")
a = 11
A = dh(a) # = dh(a, G)
print()
print("Bob")
b = 13
B = dh(b)
print("-"*30)
print("Confirm")
dh(a,B)
dh(b,A)
"""
Deffie-Hellman key exchange test
(secret key -> public key)
===========================
Alice: 71 ( 11) -> 7
Bob: 71 ( 13) -> 12
---------------------------
Confirm
A: 12 ( 11) -> 6
B: 7 ( 13) -> 6
"""Alice i Bob si vygenerují veřejné klíče A=7=Ha, B=12=Hb, které si mezi sebou vymění a ověří si,
že jim vyjde stejné ověřovací číslo S – v příkladě 6.
sk … secret key (soukromý klíč)
pk … public key (veřejný klíč)
g … generator (výchozí bod – „vhodně zvolený“, ideálně ord(g)=|G| // elements of Group)
Alice: pokud Bobovi vyjde stejné kontrolní číslo, jako vyšlo mě, můžu mu věřit, že vlastní privátní klíč.dh(a,B) = dh(b,A) -> B bylo podepsáno klíčem b, který Bob „asi“ zná. (A naopak – s Alicí)
Je to logické, protože i když nikdo nezná sk protistrany (a, b), ověří, že je to „ok“:
Alice: Hba = (Gb)a = Gba = S
Bob: Hab = (Ga)b = Gab = S
Python | Github | Defiie-Hellman:
https://github.com/agama-point/agama_point_crypto/blob/main/simple_dh_keys.py
Je dobré se zmínit i o „zero-knowledge proof“ (důkaz s nulovou znalostí) – je kryptografický protokol, který umožňuje jedné straně doložit, že má určitou informaci, aniž by tuto informaci skutečně odhalila. Tento protokol je užitečný v oblasti kybernetické bezpečnosti a digitálních transakcí, protože umožňuje ověření identity nebo pravdivosti nějakých údajů bez nutnosti odhalení samotných údajů.
V základním schématu zero-knowledge proof jedna strana (prover) potřebuje prokázat druhé straně (verifier), že má určitou znalost, aniž by tuto znalost odhalila. To se děje pomocí interakce mezi proverem a verifierem, kde prover poskytuje důkazy, které jsou ověřitelné, ale neobsahují žádné užitečné informace, kromě toho, že potvrzují platnost tvrzení.
Dalo by se takto dokázat Bobovi, že Alice má privátní klíč a, pokud mu poskytne svůj veřejný klíč A a podepsaný veřejný klíč B, patřící Bobovi.
Ještě jen pro připomenutí cykličnosti modulo:
for i in range(100):
m3 = i % 3
m5 = i % 5
m7 = i % 7
m11 = i % 11
m13 = i % 13
print(i, m3, m5, m7, m11, m13)
------------------------------------------
mod
-- 3 5 7 11 13
78 0 3 1 1 0
79 1 4 2 2 1
80 2 0 3 3 2
81 0 1 4 4 3
82 1 2 5 5 4
83 2 3 6 6 5
84 0 4 0 7 6
85 1 0 1 8 7
86 2 1 2 9 8
87 0 2 3 10 9
88 1 3 4 0 10
89 2 4 5 1 11
90 0 0 6 2 12
91 1 1 0 3 0
92 2 2 1 4 1
93 0 3 2 5 2
94 1 4 3 6 3
95 2 0 4 7 4
96 0 1 5 8 5
97 1 2 6 9 6
98 2 3 0 10 7
99 0 4 1 0 8
-> mod 17 je cyklická "po 17-ti" / cykličnost jako na hodinkách (á 12 hod) možno uzavřít do kruhu
V aritmetice modulo se cyklická povaha projevuje v tom, že modulo operace produkuje zbytek po dělení, který se může cyklicky opakovat s rostoucím číslem, pokud použijeme stejný modul.
V ukázce je vidět část řady mod 3, mod 5, mod 7, mod 11 a mod 13.
V teorii grup je cyklická grupa definována jako grupa, která je generována jedním prvkem, nazývaným generátor, a ve které opakujeme operace s tímto prvkem, abychom dosáhli všech prvků v grupě. V případě modulo operace můžeme vidět podobnost s cyklickou grupou, kde se prvky vrací do původního stavu po určitém počtu operací.
Group Theory:
https://onyb.gitbook.io/roll-your-own-crypto/group-theory
https://asecuritysite.com/blog/2022-01-04_Pallas-and-Elliptic-Curves-f34115904b02.html
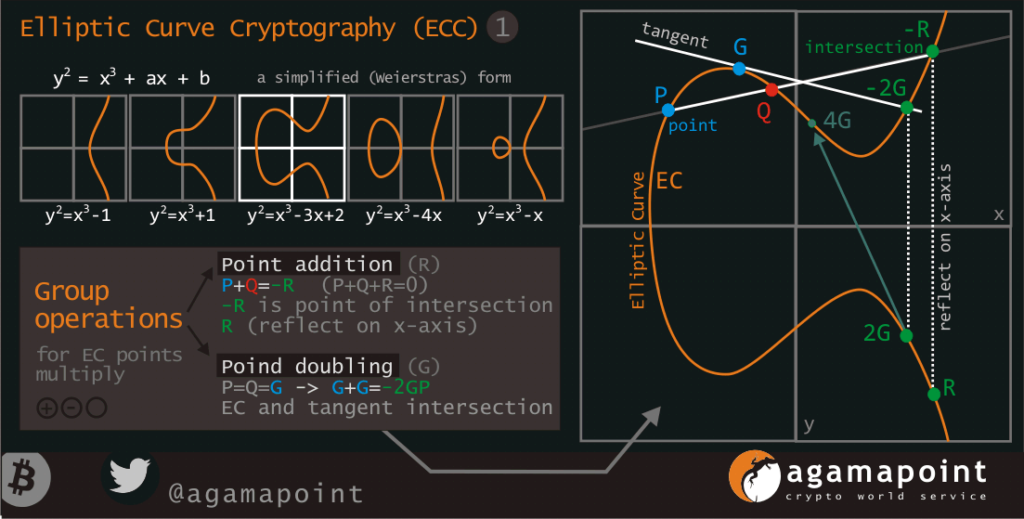
Srovnání Deffie-Hellman vs ECC:
--- DH --- + --- EC --- | 2380 bit | 228 bit --------------+--------------- G represent secret as a number | as a point--------------+---------------
Gn mod p = Hn ………….. nG = Hn
m * m * m * … …………… P dot P dot … (with a discrete field)
https://gist.github.com/onyb/cf795c819fdf8aa6015de2772fde24de
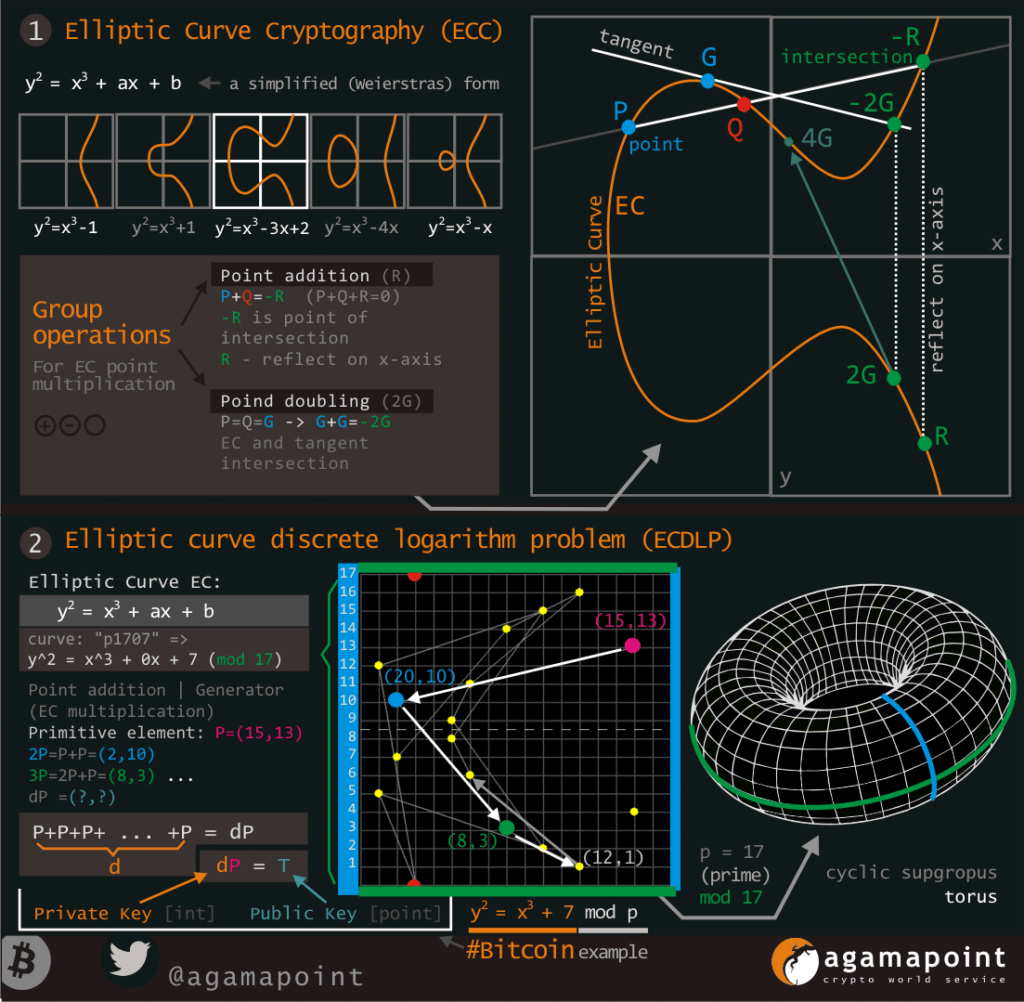
Zjednodušená verze pro „mod17“ – s P(15,13)
a, b = 0, 7
p = 17
for y in range(p+1):
for x in range(p+1):
temp = (y*y - x*x*x - a*x- b)
if(temp % p == 0):
print("* ",end="")
else:
print(". ",end="")
print()
"""
--- mod17 ---
. . . * . . . . . . . . . . . . . .
. . . . . . . . . . . . * . . . . .
. . . . . . . . . . * . . . . . . .
. . . . . . . . * . . . . . . . . .
. . . . . . . . . . . . . . . * . .
. * . . . . . . . . . . . . . . . .
. . . . . . * . . . . . . . . . . .
. . * . . . . . . . . . . . . . . .
. . . . . * . . . . . . . . . . . .
. . . . . * . . . . . . . . . . . .
. . * . . . . . . . . . . . . . . .
. . . . . . * . . . . . . . . . . .
. * . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . * . .
. . . . . . . . * . . . . . . . . .
. . . . . . . . . . * . . . . . . .
. . . . . . . . . . . . * . . . . .
. . . * . . . . . . . . . . . . . .github / python src: github.com/agama-point/agama_point_crypto/blob/main/test_elliptic1_pygame.py
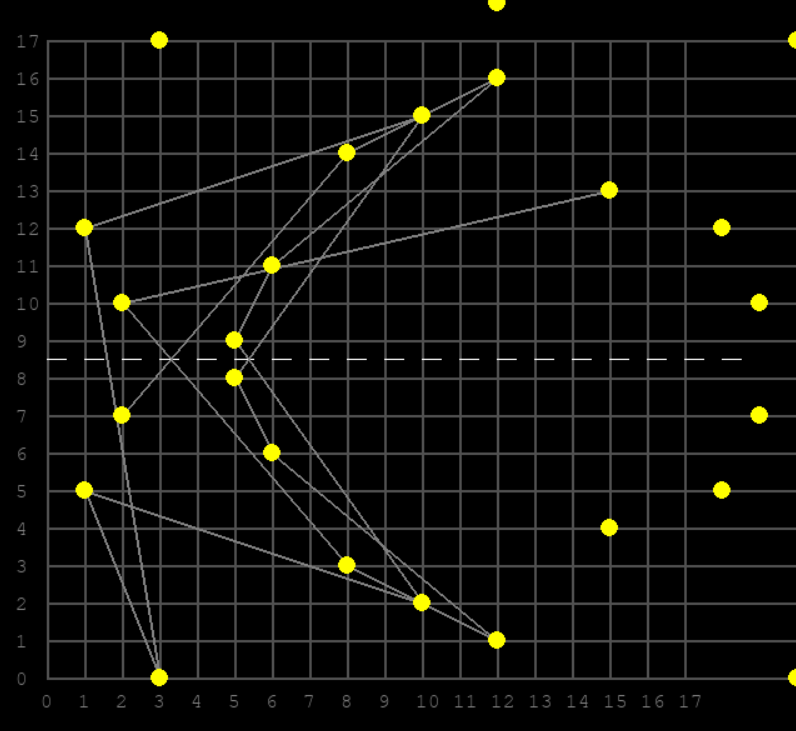
Pro malé prvočíslo pro mod je zobrazení jednoduché a transparentní.
V žádném případě by nemohlo by sloužit k „šifrování“, jelikož počet „bodů“ je velmi omezený a bruteforcem jde rozlousknout během jediné vteřiny i s omezeném, že získáme více potenciálních řešení.
(15, 13):
>>> (15*15*15-13*13+7)%17
0
--- tiny-ec --- SubGroup curve: "p1707" => y^2 = x^3 + 0x + 7 (mod 17)
ADDING
0 * G' = (None, None)
1 * G' = (15, 13)
2 * G' = (2, 10)
3 * G' = (8, 3)
4 * G' = (12, 1)
5 * G' = (6, 6)
6 * G' = (5, 8)
7 * G' = (10, 15)
8 * G' = (1, 12)
9 * G' = (3, 0)
10 * G' = (1, 5)
11 * G' = (10, 2)
12 * G' = (5, 9)
13 * G' = (6, 11)
14 * G' = (12, 16)
15 * G' = (8, 14)
16 * G' = (2, 7)
17 * G' = (15, 4)
18 * G' = (None, None)
19 * G' = (15, 13)
20 * G' = (2, 10)
21 * G' = (8, 3)
22 * G' = (12, 1)
23 * G' = (6, 6)
24 * G' = (5, 8)
25 * G' = (10, 15)
26 * G' = (1, 12)
27 * G' = (3, 0)
28 * G' = (1, 5)
29 * G' = (10, 2)
30 * G' = (5, 9)
31 * G' = (6, 11)
32 * G' = (12, 16)
...
--- agama ecc lib ---
DOUBLING
2 .. (2, 10)
4 .. (12, 1)
8 .. (1, 12)
16 .. (2, 7)
32 .. (12, 16)
64 .. (1, 5)
128 .. (2, 10)
256 .. (12, 1)
512 .. (1, 12)
1024 .. (2, 7)
2048 .. (12, 16)
4096 .. (1, 5)
8192 .. (2, 10)
16384 .. (12, 1)
32768 .. (1, 12)
...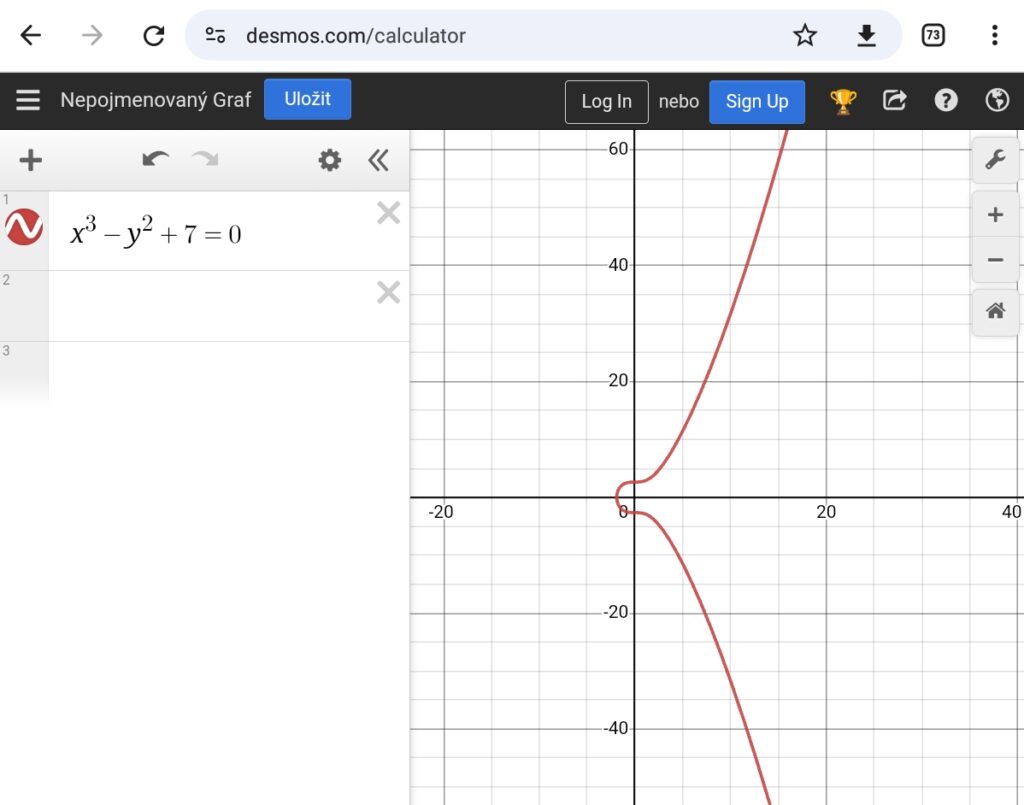
Bitcoin – secp256k1
Curve: secp256k1 ==================== G:(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8) Bit size: 256 order: 115792089237316195423570985008687907852837564279074904382605163141518161494337 p: = (2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 -1) = (2**256 - 2**32 - 977) = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f=115792089237316195423570985008687907853269984665640564039457584007908834671663 ... len(int(p)) = 78 | 17 x 17 cm versus "the universe is too small" ~ Proxima centauri 3,99×10**13km = *10**9m -> 10**22 ~ pulsar ULAS J1342+0928 1.239×10**14km -> 10**23 mm! a: 0 b: 7 =========== and where the field (p) is the prime number used with: y² = x³ +7 (mod p)
Q = (55066263022277343669578718895168534326250603453777594175500187360389116729240,
32670510020758816978083085130507043184471273380659243275938904335757337482424)
p = (2**256 - 2**32 - 977)
x, y = Q[0], Q[1]
xx = (x ** 3 + 7 - y**2) % p
print(xx)
> 0Důkaz že bod Q leží na eliptické křivce y² = x³ +7 a splňuje podmínku s (mod p) | secp256k1
(x³ – y² +7) mod p = 0
Po dosazení do rovnice získáme nulu.
https://github.com/agama-point/agama_point_crypto/blob/main/test_ecdsa_points_pygame.py
V kryptografii je používání modulo operace s velkým prvočíslem často preferované z několika důvodů:
- Jednoznačnost a neinvertibilita: Když používáme modulo s prvočíslem p, výsledek je vždy v rozsahu od 0 do p-1. Tento rozsah je jednoznačný a neinvertibilní, což znamená, že nemůžete jednoznačně zpětně získat vstupní hodnotu, pokud znáte pouze výsledek a prvočíslo. (Grupa je tímto uzavřená v max rozsahu p – výsledky prováděných operací zůstávání uvniř množiny)
- Homogenita: Používání prvočísel umožňuje matematickou homogenitu v kryptografických operacích. To znamená, že algoritmy mohou být navrženy tak, aby byly aplikovatelné na libovolná prvočísla, což zvyšuje flexibilitu a škálovatelnost kryptografických postupů.
- Omezení faktorizačního útoku: Prvočísla poskytují ochranu proti faktorizačním útokům, což jsou techniky používané k rozložení čísel na jednodušší faktory. Používání prvočíselního modulu v asymetrických šifrovacích systémech, jako je RSA, ztěžuje faktorizační útoky a zvyšuje bezpečnost šifrování.
To vše má za následek vysokou bezpečnost: Modulo operace s prvočíslem může být součástí kryptografických hashovacích funkcí, digitálních podpisů, asymetrického šifrování a dalších kryptografických operací. Prvočísla poskytují vyšší úroveň náročnosti pro prolomení šifrování a ochranu před různými útoky, jako jsou faktorizační útoky.
Počet bodů pro velké prvočíslo je „relativně malý“ a my potřebujeme nějakým způsobem generovat další a další body, ležící na křivce. Proto využijeme některé vymoženosti z teorie grup.
Grupa je v matematice sada prvků, které mají nějaké vlastnosti. Jednou z vlastností, kterou může skupina mít, je to, jak se chovají při sčítání. Když sčítáme čísla, obvykle se nám výsledek nemění, když zaměníme pořadí čísel. Například, 2+3 je totéž jako 3+2 Toto pravidlo, že výsledek sčítání se nemění, když zaměníme pořadí, se nazývá komutativní vlastnost.
Tak když mluvíme o Abelově grupě, říkáme, že všechny prvky v této skupině se chovají podobně jako čísla při sčítání. Když sečteme dva prvky v libovolném pořadí, výsledek je vždy stejný.
Abelova grupa je matematická struktura, která splňuje několik klíčových vlastností. Obecně definujeme Abelovu grupu následovně:
- Množina prvků: Abelova grupa ( (G, +) ) je množina ( G ) prvků spolu s binární operací ( + ), která je definována pro každý pár prvků ( a, b ) z ( G ). Tato operace je často nazývána jako sčítání, ale může to být libovolná operace, která splňuje určité podmínky.
- Uzavřenost: Pro libovolné prvky ( a ) a ( b ) v ( G ) platí, že výsledek ( a + b ) je opět prvkem množiny ( G ). Jinými slovy, operace sčítání zůstává uvnitř této množiny.
- Asociativita: Pro libovolné prvky ( a ), ( b ) a ( c ) v ( G ) platí, že ( (a + b) + c = a + (b + c) ). Pořadí, v jakém provádíme operace sčítání, neovlivňuje výsledek.
- Existence neutrálního prvku: Existuje prvek ( e ) v ( G ), nazývaný neutrální prvek, pro který platí, že pro každý prvek ( a ) v ( G ) platí ( a + e = e + a = a ).
- Existence inverzního prvku: Pro každý prvek ( a ) v ( G ) existuje prvek ( b ) v ( G ), nazývaný inverzní prvek, pro který platí ( a + b = b + a = e ), kde ( e ) je neutrální prvek.
- Komutativita: Tato vlastnost říká, že pro libovolné dva prvky ( a ) a ( b ) v ( G ) platí ( a + b = b + a ).
Pokud skupina splňuje všechny tyto vlastnosti, nazýváme ji Abelovou grupou. Tyto grupy jsou pojmenovány po norském matematikovi Nielsi Henrikovi Abelovi, který se zabýval studiem vlastností grup a polynomů.
Python – AES
AES (Advanced Encryption Standard – standard pokročilého šifrování) funguje na blokovém šifrování, kde text je rozdělen do bloků a každý blok je šifrován nezávisle na ostatních blocích. AES pracuje s bloky o velikosti 128 bitů a umožňuje použít klíče o délce 128, 192 nebo 256 bitů.
AES je mnohem komplexnější než substituční šifry, a to díky tomu, že provádí komplexní matematické operace na datech, které jsou důkladně navrženy tak, aby odolaly různým útokům. AES je považován za jednu z nejspolehlivějších metod symetrického šifrování v dnešní době.
Wiki: Jedná se o symetrickou blokovou šifru šifrující i dešifrující stejným klíčem data rozdělená do bloků pevně dané délky. Norma nahradila dříve užívanou šifru DES. Je používána například pro bezdrátové Wi-Fi sítě v rámci zabezpečení WPA2 dle standardu IEEE 802.11i.
from Crypto.Cipher import AES from Crypto.Util.Padding import pad, unpad # Definujeme veřejné parametry G = 2 # Generátor n = 17 # Modulo prvočíslo # Alice a Bob si zvolí své soukromé klíče a = 5 # Soukromý klíč Alice b = 3 # Soukromý klíč Bob # Výpočet veřejných klíčů A = (G ** a) % n # >>> 15 B = (G ** b) % n # >>> 8# 2 ** 3 = 8, 8 % 17 = 8 , pokud se vejdem do n - zůstáváme x# Výpočet společného klíče s_Alice = (B ** a) % n## (8**5)%17 = 32768%17 = 9>>> 9s_Bob = (A ** b) % n#>>> 9# Kontrola, zda mají oba stejný společný klíč print("společný klíč:", s_Alice, s_Bob) assert s_Alice == s_Bob # Symetrické šifrování a dešifrování def encrypt_message(message, key): cipher = AES.new(key, AES.MODE_ECB) ciphertext = cipher.encrypt(pad(message.encode(), AES.block_size)) return ciphertext def decrypt_message(ciphertext, key): cipher = AES.new(key, AES.MODE_ECB) decrypted_message = unpad(cipher.decrypt(ciphertext), AES.block_size) return decrypted_message.decode() # Vytvoření symetrického klíče ze společného klíče symmetric_key = str(s_Alice).zfill(16)[:16].encode() print("symmetric_key:", symmetric_key) print("============================================================") # Zpráva od Alice pro Boba message = "agama test" # Zašifrování zprávy encrypted_message = encrypt_message(message, symmetric_key) print("Zašifrovaná zpráva:", encrypted_message) # Dešifrování zprávy Bobem decrypted_message = decrypt_message(encrypted_message, symmetric_key) print("Dešifrovaná zpráva:", decrypted_message)>>> symmetric_key: b'0000000000000009' Zašifrovaná zpráva: b'\x0f\x8d\xdb\\\xfb\xb1\xb6psC\xe1\xc6\x7fC\xfa\xf1' Dešifrovaná zpráva: agama test ------------------------------------------- Trochu větší čísla: M61 2305843009213693951 G, n : 123 2305843009213693951 [soukromé klíče] a, b : 555555 333333 [veřejné klíče] A, B : 211374324520908086 | 1299304364174442879 společný klíč: 1218587774255145983 ok HEX: 0x10e94b1fd41ca3ff AES.block_size 16 hex_symmetric_key: 0x10e94b1fd41ca3ff | b'10e94b1fd41ca3ff' =========================================== Zašifrovaná zpráva: 8629604f4651ae892fa179e146251d85bd63e561395c351ff9fdb2afa0061f157cf256f4af18719e233067b733489b8c3bae8b6cba0e2c6191f93d6289829426e87f2a1e050981d0e9e266cc242b5006 Dešifrovaná zpráva: agama test 567 - a něco navíc? příliš žluťoučký kůň... například
AES je určen pro šifrování dat, zatímco PGP (Pretty Good Privacy) je komplexnější nástroj, který poskytuje možnosti šifrování, digitálního podepisování a správy klíčů pro komunikaci, zejména v kontextu e-mailové komunikace. Právě proto je PGP široce používán pro zabezpečení elektronické komunikace a ochranu soukromí.
(PGP je hybridní kryptografický systém, který kombinuje symetrické a asymetrické šifrování – používá asymetrickou šifru pro výměnu symetrických klíčů.)
Python – cryptos
https://github.com/primal100/pybitcointools
…
>>> from cryptos import * >>> b = Bitcoin() >>> dir(b) [' ... 'address_prefixes', 'addrtoscript', 'block_height', 'block_info', 'client', 'client_kwargs', 'coin_symbol', 'current_block_height', 'display_name', 'electrum_address', 'electrum_wallet', 'electrum_xprv_headers', 'electrum_xpub_headers', 'enabled', 'encode_privkey', 'explorer', 'fetchtx', 'hash_to_segwit_addr', 'hashcode', 'hd_path', 'history', 'inspect', 'is_address', 'is_p2sh', 'is_segwit', 'is_testnet', 'magicbyte', 'merkle_prove', 'mk_multsig_address', 'mksend', 'mktx', 'multisign', 'output_script_to_address', 'p2sh_scriptaddr', 'p2wpkh_p2sh_wallet', 'p2wpkh_wallet', 'preparemultitx', 'preparesignedmultitx', 'preparesignedtx', 'preparetx', 'privtoaddr', 'privtop2w', 'privtopub', 'privtosegwit', 'pubtoaddr', 'pubtop2w', 'pubtosegwit', 'pushtx', 'rpc_client', 'script_magicbyte', 'script_prefixes', 'script_to_p2wsh', 'scripttoaddr', 'secondary_hashcode', 'segwit_hrp', 'segwit_supported', 'send', 'sendmultitx', 'sign', 'signall', 'testnet_overrides', 'txinputs', 'unspent', 'wallet', 'watch_electrum_p2wpkh_wallet', 'watch_electrum_wallet', 'watch_p2wpkh_p2sh_wallet', 'watch_p2wpkh_wallet', 'watch_wallet', 'wif_prefix', 'wif_script_types', 'xprv_headers', 'xpub_headers'] -------------------------------------------- >>> from cryptos import * >>> b = Bitcoin() >>> from priv_data import words_book >>> wallet = b.wallet(words_book) >>> dir(wallet) ['... 'account', 'addresses', 'balance', 'change_address', 'change_addresses', 'coin', 'details', 'export_privkeys', 'history', 'is_change', 'is_mine', 'is_watching_only', 'keystore' (.xprv, .xpub), 'last_change_index', 'last_receiving_index', 'mksend', 'new_change_address', 'new_change_address_range', 'new_change_addresses', 'new_receiving_address', 'new_receiving_address_range', 'new_receiving_addresses', 'privkey', 'pubkey_change', 'pubkey_receiving', 'pubtoaddr', 'receiving_address', 'receiving_addresses', 'script_type', 'select', 'sign', 'sign_message', 'unspent']
agamapoint.com/bip39/ | https://iancoleman.io/bip39/
genesis block
00000000 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 ................
00000010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 ................
00000020 00 00 00 00 3B A3 ED FD 7A 7B 12 B2 7A C7 2C 3E ....;£íýz{.²zÇ,>
00000030 67 76 8F 61 7F C8 1B C3 88 8A 51 32 3A 9F B8 AA gv.a.È.ÈŠQ2:Ÿ¸ª
00000040 4B 1E 5E 4A 29 AB 5F 49 FF FF 00 1D 1D AC 2B 7C K.^J)«_Iÿÿ...¬+|
00000050 01 01 00 00 00 01 00 00 00 00 00 00 00 00 00 00 ................
00000060 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 ................
00000070 00 00 00 00 00 00 FF FF FF FF 4D 04 FF FF 00 1D ......ÿÿÿÿM.ÿÿ..
00000080 01 04 45 54 68 65 20 54 69 6D 65 73 20 30 33 2F ..EThe Times 03/
00000090 4A 61 6E 2F 32 30 30 39 20 43 68 61 6E 63 65 6C Jan/2009 Chancel
000000A0 6C 6F 72 20 6F 6E 20 62 72 69 6E 6B 20 6F 66 20 lor on brink of
000000B0 73 65 63 6F 6E 64 20 62 61 69 6C 6F 75 74 20 66 second bailout f
000000C0 6F 72 20 62 61 6E 6B 73 FF FF FF FF 01 00 F2 05 or banksÿÿÿÿ..ò.
000000D0 2A 01 00 00 00 43 41 04 67 8A FD B0 FE 55 48 27 *....CA.gŠý°þUH'
000000E0 19 67 F1 A6 71 30 B7 10 5C D6 A8 28 E0 39 09 A6 .gñ¦q0·.\Ö¨(à9.¦
000000F0 79 62 E0 EA 1F 61 DE B6 49 F6 BC 3F 4C EF 38 C4 ybàê.aÞ¶Iö¼?Lï8Ä
00000100 F3 55 04 E5 1E C1 12 DE 5C 38 4D F7 BA 0B 8D 57 óU.å.Á.Þ\8M÷º..W
00000110 8A 4C 70 2B 6B F1 1D 5F AC 00 00 00 00 ŠLp+kñ._¬....Bitcoin CORE
https://www.agamapoint.com/satoshi/btc_core_v0_1.html
https://github.com/Maguines/Bitcoin-v0.1
https://developer.bitcoin.org/
Kvantové počítače?
…vzhledem k rozsahu – celé přesunuto na samostatnou stránku kvantové počítače 😉
a ukázky kódu v githubu:
https://github.com/octopusengine/quantum_computing/tree/main/qiskit
Bitcoin in Go: https://github.com/btcsuite
Bitcoin v RUSTu: github.com/rust-bitcoin/rust-bitcoin


